Curve Fitting¶
Reference¶
SAS/OR example: http://go.documentation.sas.com/?docsetId=ormpex&docsetTarget=ormpex_ex11_toc.htm&docsetVersion=15.1&locale=en
SAS/OR code for example: http://support.sas.com/documentation/onlinedoc/or/ex_code/151/mpex11.html
Model¶
import sasoptpy as so
import pandas as pd
def test(cas_conn, sols=False):
# Upload data to server first
xy_raw = pd.DataFrame([
[0.0, 1.0],
[0.5, 0.9],
[1.0, 0.7],
[1.5, 1.5],
[1.9, 2.0],
[2.5, 2.4],
[3.0, 3.2],
[3.5, 2.0],
[4.0, 2.7],
[4.5, 3.5],
[5.0, 1.0],
[5.5, 4.0],
[6.0, 3.6],
[6.6, 2.7],
[7.0, 5.7],
[7.6, 4.6],
[8.5, 6.0],
[9.0, 6.8],
[10.0, 7.3]
], columns=['x', 'y'])
xy_data = cas_conn.upload_frame(xy_raw, casout={'name': 'xy_data',
'replace': True})
# Read observations
from sasoptpy.actions import read_data
POINTS = so.Set(name='POINTS')
x = so.ParameterGroup(POINTS, name='x')
y = so.ParameterGroup(POINTS, name='y')
read_st = read_data(
table=xy_data,
index={'target': POINTS, 'key': so.N},
columns=[
{'target': x, 'column': 'x'},
{'target': y, 'column': 'y'}
]
)
# Parameters and variables
order = so.Parameter(name='order')
beta = so.VariableGroup(so.exp_range(0, order), name='beta')
estimate = so.ImplicitVar(
(beta[0] + so.expr_sum(beta[k] * x[i] ** k
for k in so.exp_range(1, order))
for i in POINTS), name='estimate')
surplus = so.VariableGroup(POINTS, name='surplus', lb=0)
slack = so.VariableGroup(POINTS, name='slack', lb=0)
objective1 = so.Expression(
so.expr_sum(surplus[i] + slack[i] for i in POINTS), name='objective1')
abs_dev_con = so.ConstraintGroup(
(estimate[i] - surplus[i] + slack[i] == y[i] for i in POINTS),
name='abs_dev_con')
minmax = so.Variable(name='minmax')
objective2 = so.Expression(minmax + 0.0, name='objective2')
minmax_con = so.ConstraintGroup(
(minmax >= surplus[i] + slack[i] for i in POINTS), name='minmax_con')
order.set_init(1)
L1 = so.Model(name='L1', session=cas_conn)
L1.set_objective(objective1, sense=so.MIN, name='L1obj')
L1.include(POINTS, x, y, read_st)
L1.include(order, beta, estimate, surplus, slack, abs_dev_con)
L1.add_postsolve_statement('print x y estimate surplus slack;')
L1.solve(verbose=True)
if sols:
sol_data1 = L1.response['Print1.PrintTable'].sort_values('x')
print(so.get_solution_table(beta))
print(sol_data1.to_string())
Linf = so.Model(name='Linf', session=cas_conn)
Linf.include(L1, minmax, minmax_con)
Linf.set_objective(objective2, sense=so.MIN, name='Linfobj')
Linf.solve()
if sols:
sol_data2 = Linf.response['Print1.PrintTable'].sort_values('x')
print(so.get_solution_table(beta))
print(sol_data2.to_string())
order.set_init(2)
L1.solve()
if sols:
sol_data3 = L1.response['Print1.PrintTable'].sort_values('x')
print(so.get_solution_table(beta))
print(sol_data3.to_string())
Linf.solve()
if sols:
sol_data4 = Linf.response['Print1.PrintTable'].sort_values('x')
print(so.get_solution_table(beta))
print(sol_data4.to_string())
if sols:
return (sol_data1, sol_data2, sol_data3, sol_data4)
else:
return Linf.get_objective_value()
Output¶
In [1]: import os
In [2]: hostname = os.getenv('CASHOST')
In [3]: port = os.getenv('CASPORT')
In [4]: from swat import CAS
In [5]: cas_conn = CAS(hostname, port)
In [6]: import sasoptpy
In [7]: from examples.server_side.curve_fitting import test
In [8]: (s1, s2, s3, s4) = test(cas_conn, sols=True)
NOTE: Cloud Analytic Services made the uploaded file available as table XY_DATA in caslib CASUSER(casuser).
NOTE: The table XY_DATA has been created in caslib CASUSER(casuser) from binary data uploaded to Cloud Analytic Services.
NOTE: Initialized model L1.
NOTE: Added action set 'optimization'.
NOTE: Converting model L1 to OPTMODEL.
set POINTS;
num x {POINTS};
num y {POINTS};
read data XY_DATA into POINTS=[_N_] x y;
num order init 1;
var beta {{0..order}};
impvar estimate {o8 in POINTS} = beta[0] + sum {k in 1..order} (beta[k] * (x[o8]) ^ (k));
var surplus {{POINTS}} >= 0;
var slack {{POINTS}} >= 0;
con abs_dev_con {o32 in POINTS} : y[o32] - estimate[o32] + surplus[o32] - slack[o32] = 0;
min L1obj = sum {i in POINTS} (surplus[i] + slack[i]);
solve;
create data solution from [i]= {1.._NVAR_} var=_VAR_.name value=_VAR_ lb=_VAR_.lb ub=_VAR_.ub rc=_VAR_.rc;
create data dual from [j] = {1.._NCON_} con=_CON_.name value=_CON_.body dual=_CON_.dual;
print x y estimate surplus slack;
NOTE: Submitting OPTMODEL code to CAS server.
NOTE: There were 19 rows read from table 'XY_DATA' in caslib 'CASUSER(casuser)'.
NOTE: Problem generation will use 8 threads.
NOTE: The problem has 40 variables (2 free, 0 fixed).
NOTE: The problem uses 19 implicit variables.
NOTE: The problem has 19 linear constraints (0 LE, 19 EQ, 0 GE, 0 range).
NOTE: The problem has 75 linear constraint coefficients.
NOTE: The problem has 0 nonlinear constraints (0 LE, 0 EQ, 0 GE, 0 range).
NOTE: The OPTMODEL presolver is disabled for linear problems.
NOTE: The LP presolver value AUTOMATIC is applied.
NOTE: The LP presolver time is 0.03 seconds.
NOTE: The LP presolver removed 38 variables and 0 constraints.
NOTE: The LP presolver removed 38 constraint coefficients.
NOTE: The LP presolver formulated the dual of the problem.
NOTE: The presolved problem has 19 variables, 2 constraints, and 37 constraint coefficients.
NOTE: The LP solver is called.
NOTE: The Dual Simplex algorithm is used.
Objective
Phase Iteration Value Time
D 2 1 6.160000E+01 0
D 2 5 1.146625E+01 0
NOTE: Optimal.
NOTE: Objective = 11.46625.
NOTE: The Dual Simplex solve time is 0.06 seconds.
NOTE: The output table 'SOLUTION' in caslib 'CASUSER(casuser)' has 40 rows and 6 columns.
NOTE: The output table 'DUAL' in caslib 'CASUSER(casuser)' has 19 rows and 4 columns.
NOTE: The CAS table 'solutionSummary' in caslib 'CASUSER(casuser)' has 13 rows and 4 columns.
NOTE: The CAS table 'problemSummary' in caslib 'CASUSER(casuser)' has 18 rows and 4 columns.
beta
0 0.58125
1 0.63750
COL1 x y estimate surplus slack
10 11.0 0.0 1.0 0.58125 0.000000e+00 0.41875
18 19.0 0.5 0.9 0.90000 5.551115e-17 0.00000
12 13.0 1.0 0.7 1.21875 5.187500e-01 0.00000
4 5.0 1.5 1.5 1.53750 3.750000e-02 0.00000
0 1.0 1.9 2.0 1.79250 0.000000e+00 0.20750
15 16.0 2.5 2.4 2.17500 0.000000e+00 0.22500
1 2.0 3.0 3.2 2.49375 0.000000e+00 0.70625
11 12.0 3.5 2.0 2.81250 8.125000e-01 0.00000
5 6.0 4.0 2.7 3.13125 4.312500e-01 0.00000
3 4.0 4.5 3.5 3.45000 0.000000e+00 0.05000
8 9.0 5.0 1.0 3.76875 2.768750e+00 0.00000
14 15.0 5.5 4.0 4.08750 8.750000e-02 0.00000
13 14.0 6.0 3.6 4.40625 8.062500e-01 0.00000
7 8.0 6.6 2.7 4.78875 2.088750e+00 0.00000
9 10.0 7.0 5.7 5.04375 0.000000e+00 0.65625
17 18.0 7.6 4.6 5.42625 8.262500e-01 0.00000
2 3.0 8.5 6.0 6.00000 0.000000e+00 0.00000
6 7.0 9.0 6.8 6.31875 0.000000e+00 0.48125
16 17.0 10.0 7.3 6.95625 0.000000e+00 0.34375
NOTE: Initialized model Linf.
NOTE: Added action set 'optimization'.
NOTE: Converting model Linf to OPTMODEL.
NOTE: Submitting OPTMODEL code to CAS server.
NOTE: There were 19 rows read from table 'XY_DATA' in caslib 'CASUSER(casuser)'.
NOTE: Problem generation will use 8 threads.
NOTE: The problem has 41 variables (3 free, 0 fixed).
NOTE: The problem uses 19 implicit variables.
NOTE: The problem has 38 linear constraints (0 LE, 19 EQ, 19 GE, 0 range).
NOTE: The problem has 132 linear constraint coefficients.
NOTE: The problem has 0 nonlinear constraints (0 LE, 0 EQ, 0 GE, 0 range).
NOTE: The OPTMODEL presolver is disabled for linear problems.
NOTE: The LP presolver value AUTOMATIC is applied.
NOTE: The LP presolver time is 0.00 seconds.
NOTE: The LP presolver removed 0 variables and 0 constraints.
NOTE: The LP presolver removed 0 constraint coefficients.
NOTE: The presolved problem has 41 variables, 38 constraints, and 132 constraint coefficients.
NOTE: The LP solver is called.
NOTE: The Dual Simplex algorithm is used.
Objective
Phase Iteration Value Time
D 2 1 -1.900000E+00 0
P 2 26 1.725000E+00 0
NOTE: Optimal.
NOTE: Objective = 1.725.
NOTE: The Dual Simplex solve time is 0.01 seconds.
NOTE: The output table 'SOLUTION' in caslib 'CASUSER(casuser)' has 41 rows and 6 columns.
NOTE: The output table 'DUAL' in caslib 'CASUSER(casuser)' has 38 rows and 4 columns.
NOTE: The CAS table 'solutionSummary' in caslib 'CASUSER(casuser)' has 13 rows and 4 columns.
NOTE: The CAS table 'problemSummary' in caslib 'CASUSER(casuser)' has 18 rows and 4 columns.
beta
0 -0.400
1 0.625
COL1 x y estimate surplus slack
10 11.0 0.0 1.0 -0.4000 0.000 1.4000
18 19.0 0.5 0.9 -0.0875 0.000 0.9875
12 13.0 1.0 0.7 0.2250 0.000 0.4750
4 5.0 1.5 1.5 0.5375 0.000 0.9625
0 1.0 1.9 2.0 0.7875 0.000 1.2125
15 16.0 2.5 2.4 1.1625 0.000 1.2375
1 2.0 3.0 3.2 1.4750 0.000 1.7250
11 12.0 3.5 2.0 1.7875 0.000 0.2125
5 6.0 4.0 2.7 2.1000 0.000 0.6000
3 4.0 4.5 3.5 2.4125 0.000 1.0875
8 9.0 5.0 1.0 2.7250 1.725 0.0000
14 15.0 5.5 4.0 3.0375 0.000 0.9625
13 14.0 6.0 3.6 3.3500 0.000 0.2500
7 8.0 6.6 2.7 3.7250 1.025 0.0000
9 10.0 7.0 5.7 3.9750 0.000 1.7250
17 18.0 7.6 4.6 4.3500 0.000 0.2500
2 3.0 8.5 6.0 4.9125 0.000 1.0875
6 7.0 9.0 6.8 5.2250 0.000 1.5750
16 17.0 10.0 7.3 5.8500 0.000 1.4500
NOTE: Added action set 'optimization'.
NOTE: Converting model L1 to OPTMODEL.
NOTE: Submitting OPTMODEL code to CAS server.
NOTE: There were 19 rows read from table 'XY_DATA' in caslib 'CASUSER(casuser)'.
NOTE: Problem generation will use 8 threads.
NOTE: The problem has 41 variables (3 free, 0 fixed).
NOTE: The problem uses 19 implicit variables.
NOTE: The problem has 19 linear constraints (0 LE, 19 EQ, 0 GE, 0 range).
NOTE: The problem has 93 linear constraint coefficients.
NOTE: The problem has 0 nonlinear constraints (0 LE, 0 EQ, 0 GE, 0 range).
NOTE: The OPTMODEL presolver is disabled for linear problems.
NOTE: The LP presolver value AUTOMATIC is applied.
NOTE: The LP presolver time is 0.00 seconds.
NOTE: The LP presolver removed 38 variables and 0 constraints.
NOTE: The LP presolver removed 38 constraint coefficients.
NOTE: The LP presolver formulated the dual of the problem.
NOTE: The presolved problem has 19 variables, 3 constraints, and 55 constraint coefficients.
NOTE: The LP solver is called.
NOTE: The Dual Simplex algorithm is used.
Objective
Phase Iteration Value Time
D 2 1 6.160000E+01 0
D 2 5 1.045896E+01 0
NOTE: Optimal.
NOTE: Objective = 10.458964706.
NOTE: The Dual Simplex solve time is 0.01 seconds.
NOTE: The output table 'SOLUTION' in caslib 'CASUSER(casuser)' has 41 rows and 6 columns.
NOTE: The output table 'DUAL' in caslib 'CASUSER(casuser)' has 19 rows and 4 columns.
NOTE: The CAS table 'solutionSummary' in caslib 'CASUSER(casuser)' has 13 rows and 4 columns.
NOTE: The CAS table 'problemSummary' in caslib 'CASUSER(casuser)' has 18 rows and 4 columns.
beta
0 0.982353
1 0.294510
2 0.033725
COL1 x y estimate surplus slack
10 11.0 0.0 1.0 0.982353 0.000000e+00 0.017647
18 19.0 0.5 0.9 1.138039 2.380392e-01 0.000000
12 13.0 1.0 0.7 1.310588 6.105882e-01 0.000000
4 5.0 1.5 1.5 1.500000 -6.938894e-17 0.000000
0 1.0 1.9 2.0 1.663671 0.000000e+00 0.336329
15 16.0 2.5 2.4 1.929412 0.000000e+00 0.470588
1 2.0 3.0 3.2 2.169412 0.000000e+00 1.030588
11 12.0 3.5 2.0 2.426275 4.262745e-01 0.000000
5 6.0 4.0 2.7 2.700000 -1.110223e-16 0.000000
3 4.0 4.5 3.5 2.990588 0.000000e+00 0.509412
8 9.0 5.0 1.0 3.298039 2.298039e+00 0.000000
14 15.0 5.5 4.0 3.622353 0.000000e+00 0.377647
13 14.0 6.0 3.6 3.963529 3.635294e-01 0.000000
7 8.0 6.6 2.7 4.395200 1.695200e+00 0.000000
9 10.0 7.0 5.7 4.696471 0.000000e+00 1.003529
17 18.0 7.6 4.6 5.168612 5.686118e-01 0.000000
2 3.0 8.5 6.0 5.922353 0.000000e+00 0.077647
6 7.0 9.0 6.8 6.364706 0.000000e+00 0.435294
16 17.0 10.0 7.3 7.300000 4.440892e-16 0.000000
NOTE: Added action set 'optimization'.
NOTE: Converting model Linf to OPTMODEL.
NOTE: Submitting OPTMODEL code to CAS server.
NOTE: There were 19 rows read from table 'XY_DATA' in caslib 'CASUSER(casuser)'.
NOTE: Problem generation will use 8 threads.
NOTE: The problem has 42 variables (4 free, 0 fixed).
NOTE: The problem uses 19 implicit variables.
NOTE: The problem has 38 linear constraints (0 LE, 19 EQ, 19 GE, 0 range).
NOTE: The problem has 150 linear constraint coefficients.
NOTE: The problem has 0 nonlinear constraints (0 LE, 0 EQ, 0 GE, 0 range).
NOTE: The OPTMODEL presolver is disabled for linear problems.
NOTE: The LP presolver value AUTOMATIC is applied.
NOTE: The LP presolver time is 0.00 seconds.
NOTE: The LP presolver removed 0 variables and 0 constraints.
NOTE: The LP presolver removed 0 constraint coefficients.
NOTE: The presolved problem has 42 variables, 38 constraints, and 150 constraint coefficients.
NOTE: The LP solver is called.
NOTE: The Dual Simplex algorithm is used.
Objective
Phase Iteration Value Time
D 2 1 -1.900000E+00 0
P 2 29 1.475000E+00 0
NOTE: Optimal.
NOTE: Objective = 1.475.
NOTE: The Dual Simplex solve time is 0.01 seconds.
NOTE: The output table 'SOLUTION' in caslib 'CASUSER(casuser)' has 42 rows and 6 columns.
NOTE: The output table 'DUAL' in caslib 'CASUSER(casuser)' has 38 rows and 4 columns.
NOTE: The CAS table 'solutionSummary' in caslib 'CASUSER(casuser)' has 13 rows and 4 columns.
NOTE: The CAS table 'problemSummary' in caslib 'CASUSER(casuser)' has 18 rows and 4 columns.
beta
0 2.475
1 -0.625
2 0.125
COL1 x y estimate surplus slack
10 11.0 0.0 1.0 2.47500 1.475000 0.000000
18 19.0 0.5 0.9 2.19375 1.293750 0.000000
12 13.0 1.0 0.7 1.97500 1.275000 0.000000
4 5.0 1.5 1.5 1.81875 0.318750 0.000000
0 1.0 1.9 2.0 1.73875 0.606875 0.868125
15 16.0 2.5 2.4 1.69375 0.000000 0.706250
1 2.0 3.0 3.2 1.72500 0.000000 1.475000
11 12.0 3.5 2.0 1.81875 0.000000 0.181250
5 6.0 4.0 2.7 1.97500 0.000000 0.725000
3 4.0 4.5 3.5 2.19375 0.000000 1.306250
8 9.0 5.0 1.0 2.47500 1.475000 0.000000
14 15.0 5.5 4.0 2.81875 0.000000 1.181250
13 14.0 6.0 3.6 3.22500 0.000000 0.375000
7 8.0 6.6 2.7 3.79500 1.095000 0.000000
9 10.0 7.0 5.7 4.22500 0.000000 1.475000
17 18.0 7.6 4.6 4.94500 0.345000 0.000000
2 3.0 8.5 6.0 6.19375 0.193750 0.000000
6 7.0 9.0 6.8 6.97500 0.175000 0.000000
16 17.0 10.0 7.3 8.72500 1.425000 0.000000
# Plots
In [1]: import matplotlib.pyplot as plt
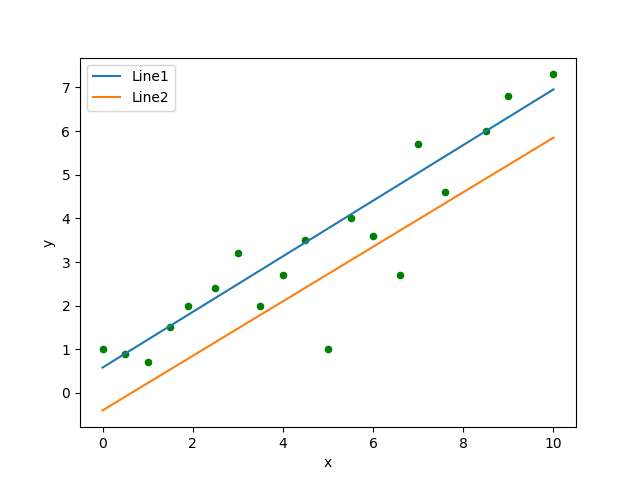
In [2]: p1 = s1.plot.scatter(x='x', y='y', c='g')
In [3]: s1.plot.line(ax=p1, x='x', y='estimate', label='Line1');
In [4]: s2.plot.line(ax=p1, x='x', y='estimate', label='Line2');
In [5]: p1
Out[5]: <matplotlib.axes._subplots.AxesSubplot at 0x7f06d1c95940>
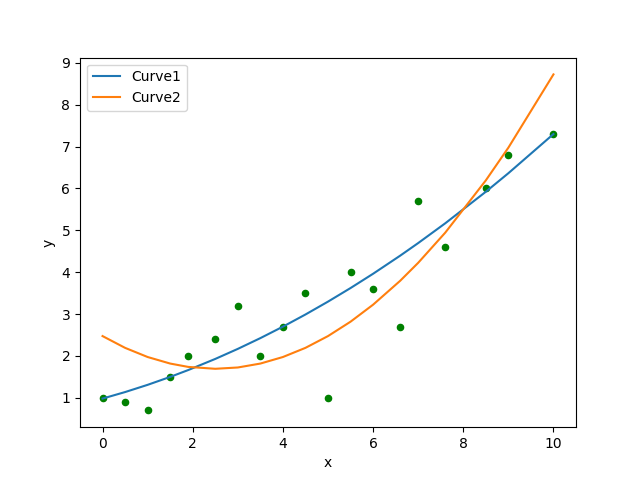
In [6]: p2 = s3.plot.scatter(x='x', y='y', c='g')
In [7]: s3.plot.line(ax=p2, x='x', y='estimate', label='Curve1');
In [8]: s4.plot.line(ax=p2, x='x', y='estimate', label='Curve2');
In [9]: p2
Out[9]: <matplotlib.axes._subplots.AxesSubplot at 0x7f06ac12a6d8>